2.1 Historic overview

2.1.1 Imputation

The English verb “to impute” comes from the Latin imputo, which means to reckon, attribute, make account of, charge, ascribe. In the Bible, the word “impute” is a translation of the Hebrew verb \({h\bar{a}shab}\), which appears about 120 times in the Old Testament in various meanings (Renn 2005). The noun “imputation” has a long history in taxation. The concept “imputed income” was used in the 19th century to denote income derived from property, such as land and housing. In the statistical literature, imputation means “filling in the data.” Imputation in this sense is first mentioned in 1957 in the work of the U.S. Census Bureau (US Bureau of the Census 1957).

Imputation is not alien to human nature. Yuval (2014) presented a world map, created in 1459 in Europe, that imputes fictitious continents in geographies that had yet to be discovered. One century later, the world map looked like a series of coastlines, with huge white spots for the inner lands, and these were all systematically explored during the later centuries. It’s only when you can admit your own ignorance that you can start learning.

Allan and Wishart (1930) were the first to develop a statistical method to replace a missing value. They provided two formulae for estimating the value of a single missing observation, and advised filling in the estimate in the data. They would then proceed as usual, but deduct one degree of freedom to correct for the missing data. Yates (1933) generalized this work to more than one missing observation, and thus planted the seeds via a long and fruitful chain of intermediates that led up to the now classic EM algorithm (Dempster, Laird, and Rubin 1977). Interestingly, the term “imputation” was not used by Dempster et al. or by any of their predecessors; it only gained widespread use after the monumental work of the Panel on Incomplete Data in 1983. Volume 2 devoted about 150 pages to an overview of the state-of-the-art of imputation technology (Madow, Olkin, and Rubin 1983). This work is not widely known, but it was the predecessor to the first edition of Little and Rubin (1987), a book that established the term firmly in the mainstream statistical literature.

2.1.2 Multiple imputation

Multiple imputation is now accepted as the best general method to deal with incomplete data in many fields, but this was not always the case. Multiple imputation was developed by Donald B. Rubin in the 1970’s. It is useful to know a bit of its remarkable history, as some of the issues in multiple imputation may resurface in contemporary applications. This section details historical observations that provide the necessary background.

The birth of multiple imputation has been documented by Fritz Scheuren (Scheuren 2005). Multiple imputation was developed as a solution to a practical problem with missing income data in the March Income Supplement to the Current Population Survey (CPS). In 1977, Scheuren was working on a joint project of the Social Security Administration and the U.S. Census Bureau. The Census Bureau was then using (and still does use) a hot deck imputation procedure. Scheuren signaled that the variance could not be properly calculated, and asked Rubin what might be done instead. Rubin came up with the idea of using multiple versions of the complete dataset, something he had already explored in the early 1970s (Rubin 1994). The original 1977 report introducing the idea was published in 2004 in the history corner of the American Statistician (Rubin 2004b). According to Scheuren: “The paper is the beginning point of a truly revolutionary change in our thinking on the topic of missingness” (Scheuren 2004, 291).

Rubin observed that imputing one value (single imputation) for the missing value could not be correct in general. He needed a model to relate the unobserved data to the observed data, and noted that even for a given model the imputed values could not be calculated with certainty. His solution was simple and brilliant: create multiple imputations that reflect the uncertainty of the missing data. The 1977 report explains how to choose the models and how to derive the imputations. A low number of imputations, say five, would be enough.

The idea to create multiple versions of the data must have seemed outrageous at that time. Drawing imputations from a distribution, instead of estimating the “best” value, was a drastic departure from everything that had been done before. Rubin’s original proposal did not include formulae for calculating combined estimates, but instead stressed the study of variation because of uncertainty in the imputed values. The idea was rooted in the Bayesian framework for inference, quite different from the dominant randomization-based framework in survey statistics. Moreover, there were practical issues involved in the technique, the larger datasets, the extra works to create the model and the repeated analysis, software issues, and so on. These issues have all been addressed by now, but in 1983 Dempster and Rubin wrote: “Practical implementation is still in the developmental state” (Dempster and Rubin 1983, 8).

Rubin (1987b) provided the methodological and statistical footing for the method. Though several improvements have been made since 1987, the book was really ahead of its time and discusses the essentials of modern imputation technology. It provides the formulas needed to combine the repeated complete-data estimates (now called Rubin’s rules), and outlines the conditions under which statistical inference under multiple imputation will be valid. Furthermore, pp. 166–170 provide a description of Bayesian sampling algorithms that could be used in practice.

Tests for combinations of parameters were developed by Li et al. (1991), Li, Raghunathan, and Rubin (1991) and Meng and Rubin (1992). Technical improvements for the degrees of freedom were suggested by Barnard and Rubin (1999) and Reiter (2007). Iterative algorithms for multivariate missing data with general missing data patterns were proposed by Rubin (1987b), Schafer (1997), Van Buuren, Boshuizen, and Knook (1999), Raghunathan et al. (2001) and King et al. (2001).

In the 1990s, multiple imputation came under fire from various sides. The most severe criticism was voiced by Fay (1992). Fay pointed out that the validity of multiple imputation can depend on the form of subsequent analysis. He produced “counterexamples” in which multiple imputation systematically understated the true covariance, and concluded that “multiple imputation is inappropriate as a general purpose methodology.” Meng (1994) pointed out that Fay’s imputation models omitted important relations that were needed in the analysis model, an undesirable situation that he labeled uncongenial. Related issues on the interplay between the imputation model and the complete-data model have been discussed by Rubin (1996) and Schafer (2003).

Several authors have shown that Rubin’s estimate of the variance can be biased (Wang and Robins 1998; Robins and Wang 2000; Nielsen 2003; Kim et al. 2006). If there is bias, the estimate is usually too large. Rubin (2003) emphasized that variance estimation is only an intermediate goal for making confidence intervals, and generally not a parameter of substantive interest. He also noted that observed bias does not seem to affect the coverage of these intervals across a wide range of cases of practical interest.

The tide turned around 2005. Reviews started to appear that criticize insufficient reporting practice of the missing data in diverse fields (cf. Section 1.1.2). Nowadays multiple imputation is almost universally accepted, and in fact acts as the benchmark against which newer methods are being compared. The major statistical packages have all implemented modules for multiple imputation, so effectively the technology is implemented, almost three decades after Dempster and Rubin’s remark.

2.1.3 The expanding literature on multiple imputation

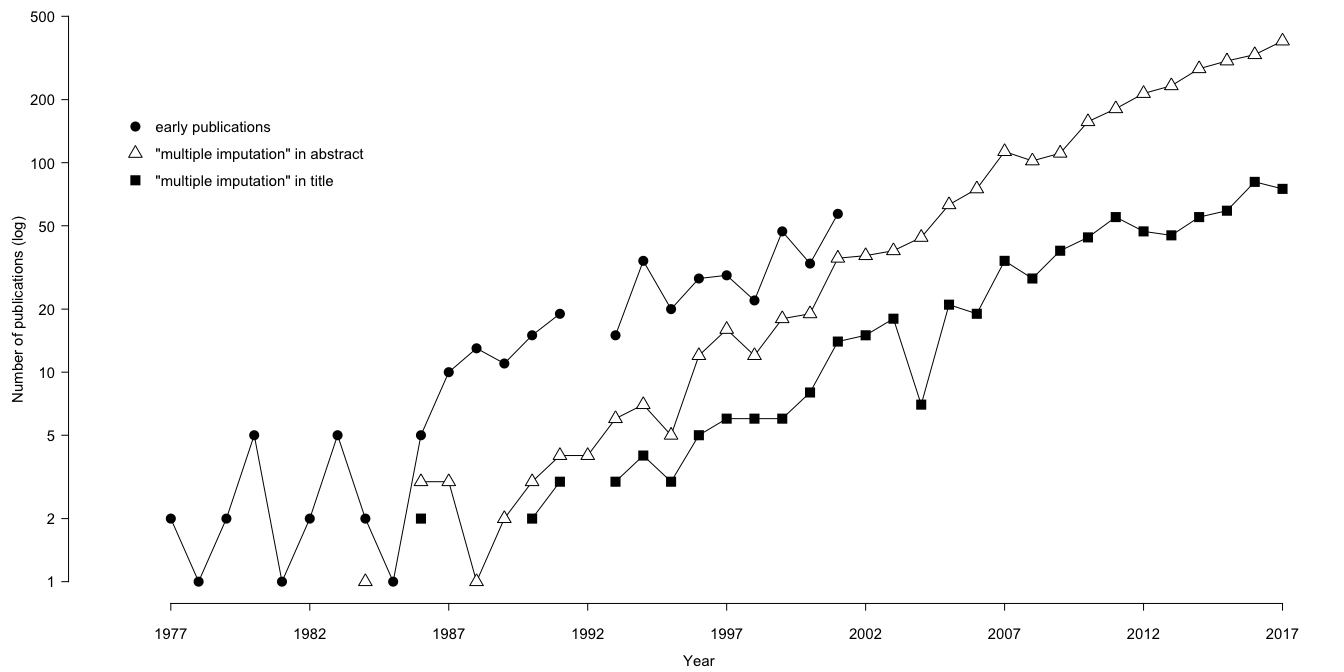
Figure 2.1: Multiple imputation at age 40. Number of publications (log) on multiple imputation during the period 1977–2017 according to three counting methods. Data source: https://www.scopus.com (accessed Jan 14, 2018).

Figure 2.1 contains three time series with counts on the number of publications on multiple imputation during the period 1977–2017. Counts were made in three ways. The rightmost series corresponds to the number of publications per year that featured the search term “multiple imputation” in the title. These are often methodological articles in which new adaptations are being developed. The series in the middle is the number of publication that featured “multiple imputation” in the title, abstract or key words in Scopus on the same search data. This set includes a growing group of papers that contain applications. The leftmost series is the number of publications in a collection of early publications available at http://www.multiple-imputation.com. This collection covers essentially everything related to multiple imputation from its inception in 1977 up to the year 2001. This group also includes chapters in books, dissertations, conference proceedings, technical reports and so on.

Note that the vertical axis is set in the logarithm. Perhaps the most interesting series is the middle series counting the applications. The pattern is approximately linear, meaning that the number of applications is growing at an exponential rate.

Several books devoted to missing data saw the light since the first edition of this book appeared in 2012. Building upon Schafer’s work, Graham (2012) provides many insightful solutions for practical issues in imputation. Carpenter and Kenward (2013) propose methodological advances on important aspects of multiple imputation. Mallinckroth (2013) and O’Kelly and Ratitch (2014) concentrate on the missing data problem in clinical trials, Zhou et al. (2014) target health sciences, whereas Kim and Shao (2013) is geared towards official statistics. The Handbook of Missing Data Methodology (Molenberghs et al. 2015) presents a broad and up-to-date technical overview of the field of missing data. Raghunathan (2015) describes a variety of applications in social sciences and health using sequential regression multivariate imputation .

In addition to papers and books, high-quality software is now available to ease application of multiple imputation in practice. Rezvan, Lee, and Simpson (2015) signal a wide adoption of multiple imputation, but warn that reporting is often substandard. Many more researchers have realized the full generality of the missing data problem. Effectively, missing data has now transformed into one of the great academic growth industries.