3.5 Classification and regression trees
3.5.1 Overview
Classification and regression trees (CART) (Breiman et al. 1984) are a popular class of machine learning algorithms. CART models seek predictors and cut points in the predictors that are used to split the sample. The cut points divide the sample into more homogeneous subsamples. The splitting process is repeated on both subsamples, so that a series of splits defines a binary tree. The target variable can be discrete (classification tree) or continuous (regression tree).
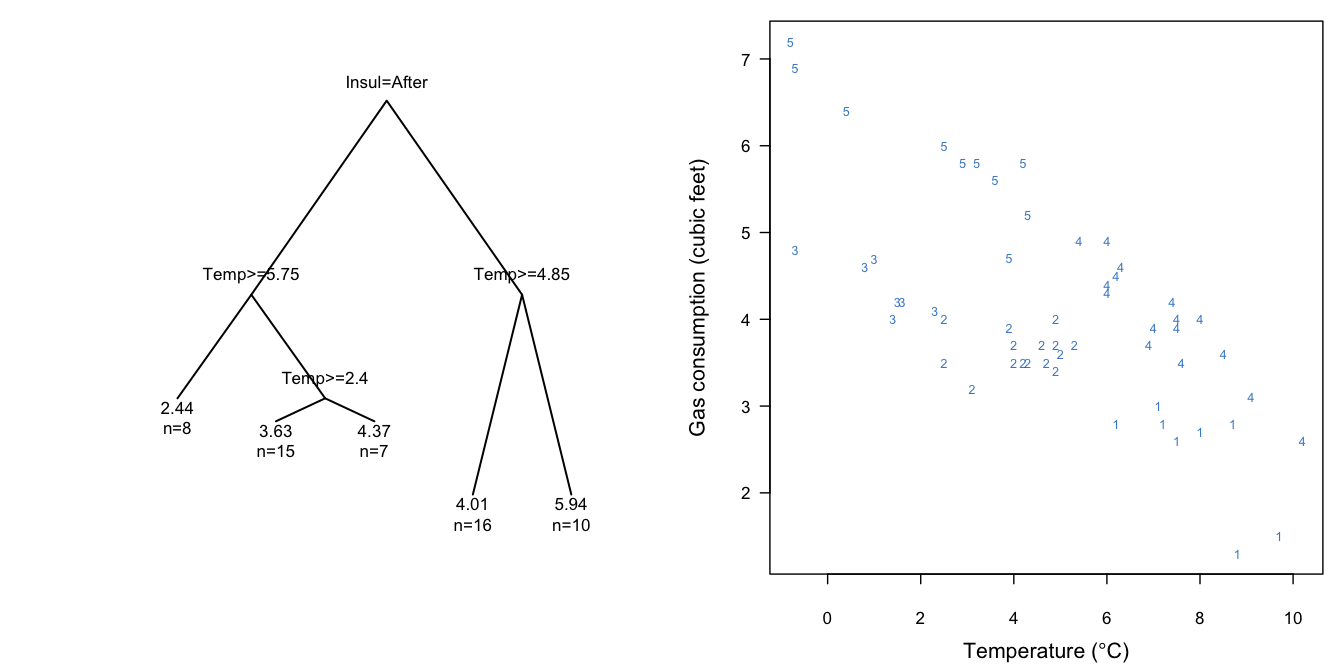
Figure 3.8: Regression tree for predicting gas consumption. The left-hand plot displays the binary tree, whereas the right-hand plot identifies the groups at each end leaf in the data.
Figure 3.8 illustrates a simple CART solution for the whiteside data. The left-hand side contains the optimal binary tree for predicting gas consumption from temperature and insulation status. The right-hand side shows the scatterplot in which the five groups are labeled by their terminal nodes.
CART methods have properties that make them attractive for imputation: they are robust against outliers, can deal with multicollinearity and skewed distributions, and are flexible enough to fit interactions and nonlinear relations. Furthermore, many aspects of model fitting have been automated, so there is “little tuning needed by the imputer” (Burgette and Reiter 2010).
The idea of using CART methods for imputation has been suggested by a wide variety of authors in a variety of ways. See Saar-Tsechansky and Provost (2007) for an introductory overview. Some investigators (He 2006; Vateekul and Sarinnapakorn 2009) simply fill in the mean or mode. The majority of tree-based imputation methods use some form of single imputation based on prediction (Bárcena and Tusell 2000; Conversano and Cappelli 2003; Siciliano, Aria, and D’Ambrosio 2006; Creel and Krotki 2006; Ishwaran et al. 2008; Conversano and Siciliano 2009). Multiple imputation methods have been developed by Harrell (2001), who combined it with optimal scaling of the input variables, by Reiter (2005b) and by Burgette and Reiter (2010). Wallace, Anderson, and Mazumdar (2010) present a multiple imputation method that averages the imputations to produce a single tree and that does not pool the variances. Parker (2010) investigates multiple imputation methods for various unsupervised and supervised learning algorithms.
The missForest method (Stekhoven and Bühlmann 2011) successfully used regression and classification trees to predict the outcomes in mixed continuous/categorical data. MissForest is popular, presumably because it produces a single complete dataset, which at the same time is the reason why it fails as a scientific method. The missForest method does not account for the uncertainty caused by the missing data, treats the imputed data as if they were real (which they are not), and thus invents information. As a consequence, \(p\)-values calculated after application of missForest will be more significant than they actually are, confidence intervals will be shorter than they actually are, and relations between variables will be stronger than they actually are. These problems worsen as more missing values are imputed. Unfortunately, comparisons studies that evaluate only accuracy, such as Waljee et al. (2013), will fail to detect these problems.
As a alternative, multiple imputations can be created using the tree in Figure 3.8. For a given temperature and insulation status, traverse the tree and find the appropriate terminal node. Form the donor group of all observed cases at the terminal node, randomly draw a case from the donor group, and take its reported gas consumption as the imputed value. The idea is identical to predictive mean matching (cf. Section 3.4), where the “predictive mean” is now calculated by a tree model instead of a regression model. As before, the parameter uncertainty can be incorporated by fitting the tree on a bootstrapped sample.
Algorithm 3.4 (Imputation under a tree model using the bootstrap.)
Draw a bootstrap sample \((\dot y_\mathrm{obs},\dot X_\mathrm{obs})\) of size \(n_1\) from \((y_\mathrm{obs},X_\mathrm{obs})\).
Fit \(\dot y_\mathrm{obs}\) by \(\dot X_\mathrm{obs}\) by a tree model \(f(X)\).
Predict the \(n_0\) terminal nodes \(g_j\) from \(f(X_\mathrm{mis})\).
Construct \(n_0\) sets \(Z_j\) of all cases at node \(g_j\), each containing \(d_j\) candidate donors.
Draw one donor \(i_j\) from \(Z_j\) randomly for \(j=1,\dots,n_0\).
- Calculate imputations \(\dot y_j = y_{i_j}\) for \(j=1,\dots,n_0\).
Algorithm 3.4 describes the major steps of an algorithm for creating imputations using a classification or regression tree. There is considerable freedom at step 2, where the tree model is fitted to the training data \((\dot y_\mathrm{obs},\dot X_\mathrm{obs})\). It may be useful to fit the tree such that the number of cases at each node is equal to some pre-set number, say 5 or 10. The composition of the donor groups will vary over different bootstrap replications, thus incorporating sampling uncertainty about the tree.
Multiple imputation methodology using trees has been developed by Burgette and Reiter (2010), Shah et al. (2014) and Doove, Van Buuren, and Dusseldorp (2014). The main motivation given in these papers was to improve our ability to account for interactions and other non-linearities, but these are generic methods that apply to both continuous and categorical outcomes and predictors. Burgette and Reiter (2010) used the tree package, and showed that the CART results for recovering interactions were uniformly better than standard techniques. Shah et al. (2014) applied random forest techniques to both continuous and categorical outcomes, which produced more efficient estimates than standard procedures. The techniques are available as methods rfcat and rfcont in the CALIBERrfimpute package. Doove, Van Buuren, and Dusseldorp (2014) independently developed a similar set of routines building on the rpart (Therneau, Atkinson, and Ripley 2017) and randomForest (Liaw and Wiener 2002) packages. Methods cart and rf are part of mice.
A recent development is the growing interest from the machine learning community for the idea of multiple imputation. The problem of imputing missing values has now been discovered by many, but unfortunately nearly all new algorithms produce single imputations. An exception is the paper by Sovilj et al. (2016), who propose the extreme learning machine using conditional Gaussian mixture models to generate multiple imputations. It is a matter of time before researchers realize the intimate connections between multiple imputation and ensemble learning, so that more work along these lines may follow.