Fitting ARMA time series by structural equation models

Abstract

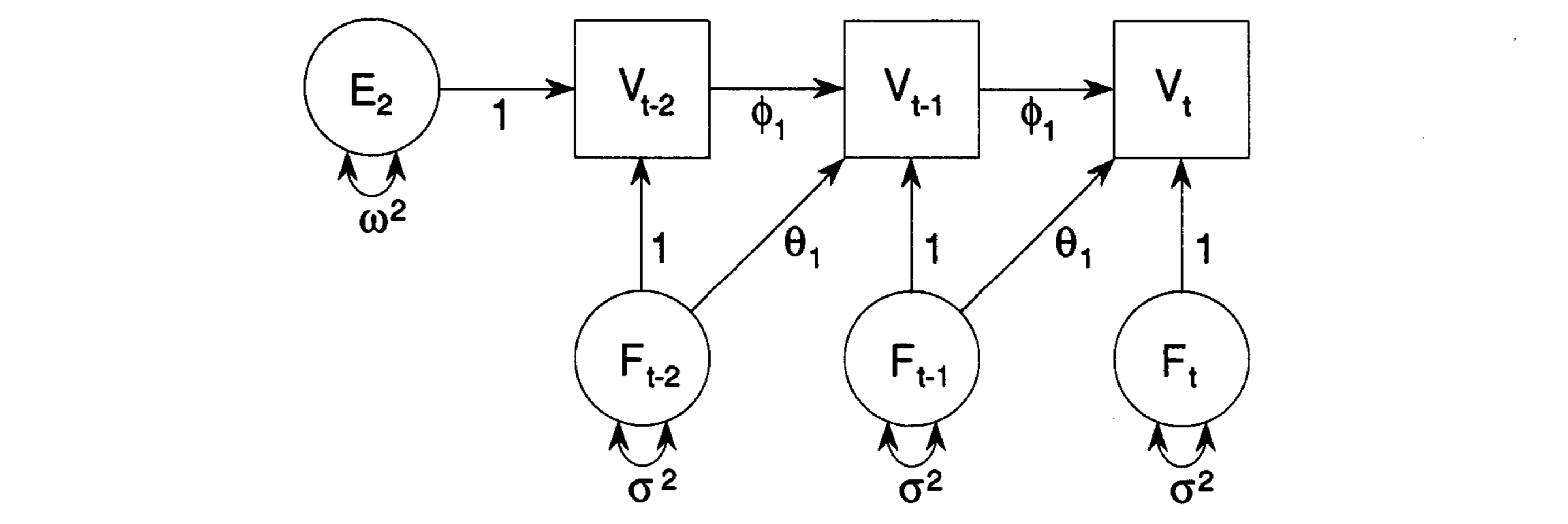
This paper outlines how the stationary ARMA(p,q) model can be specified as a structural equations model. Maximum likelihood estimates for the parameters in the ARMA model can be obtained by software for fitting structural equation models. For pure AR and mixed ARMA models, these estimates are approximately unbiased, while the efficiency is as good as those of specialized recursive estimators. The reported standard errors are generally found to be valid. Depending on sample size, estimates for pure MA models are biased 5-10% and considerably less efficient. Some assets of the method are that ARMA model parameters can be estimated when only autocovariances are known, that model constraints can be incorporated, and that the fit between observed and modelled covariances can be tested by statistical methods. The method is applied to problems that involve the evaluation of pregnancy as a function of perceived bodily changes, the effect of policy interventions in crime prevention, and the influence of weather conditions on absence from work.